commentaires
« Le marché boursier est conçu pour transférer de l’argent de l’actif au patient. » ― Warren Buffett
A voir aussi : Comprendre l'assurance auto et les chevaux fiscaux : conseils et astuces
Source : gfycat.com/
A lire en complément : Pourquoi les indices commerciaux ?
La recherche générale associée au marché boursier ou aux actions se concentre fortement sur ni l’achat ni la vente, mais elle ne tient pas compte de la dimension et de l’espérance d’un nouvel investisseur. La tendance commune au marché boursier dans la société est qu’elle est très risquée pour l’investissement ou ne convient pas au commerce, de sorte que la plupart des gens ne sont même pas intéressés. La variance saisonnière et le flux constant de tout indice aideront les investisseurs existants et naïfs à comprendre et à prendre la décision d’investir dans le marché boursier/actions.
Pour résoudre ces types de problèmes, l’analyse des séries chronologiques sera le meilleur outil pour prévoir la tendance ou même l’avenir. L’organigramme fournira des orientations adéquates à l’investisseur.
Alors, laissez-nous comprendre ce concept en détail et utiliser un apprentissage automatique technique pour prévoir les stocks.
Plan de l'article
Bourse
Une action ou une action (également appelée « capitaux propres » d’une société) est un instrument financier qui représente la propriété d’une société ou d’une société et représente une créance proportionnelle sur ses actifs (ce qu’elle possède) et ses bénéfices (ce qu’elle génère en bénéfices). — Investopedia
Le marché boursier est un marché qui permet l’échange harmonieux d’achat et de vente des actions de l’entreprise. Chaque bourse a sa propre valeur de l’indice boursier. L’indice est la valeur moyenne qui est calculée en combinant plusieurs actions. Cela aide à représenter l’ensemble du marché boursier et à prévoir l’évolution du marché au fil du temps. Le marché boursier peut avoir un impact énorme sur la population et l’économie du pays dans son ensemble. Par conséquent, prédire efficacement l’évolution des stocks peut minimiser le risque de perte et maximiser les profits.
Comment fonctionne le marché boursier ?
Le concept derrière la façon dont le fonctionne boursier est assez simple. Fonctionnant un peu comme une maison de vente aux enchères, le marché boursier permet aux acheteurs et aux vendeurs de négocier des prix et de faire des transactions.
Le marché boursier fonctionne à travers un réseau de bourses — vous avez peut-être entendu parler de la Bourse de New York, du Nasdaq ou du Sensex. Les sociétés listent des actions de leurs actions en bourse par le biais d’un processus appelé appel public initial ou introduction en bourse. Les investisseurs achètent ces actions, ce qui permet à l’entreprise de collecter des fonds pour développer son activité. Les investisseurs peuvent alors acheter et vendre ces actions entre eux, et la bourse suit l’offre et la demande de chaque action cotée.
Cette offre et la demande aident à déterminer le prix de chaque titre ou les niveaux auxquels les participants aux marchés boursiers — investisseurs et commerçants — sont prêts à acheter ou à vendre.
Comment les prix des actions sont définis
Pour acheter réellement des actions d’une bourse, les investisseurs passent par des courtiers — un intermédiaire formé à la science de le négoce boursier, qui peut obtenir un investisseur une action à un prix juste, à un moment de préavis. Les investisseurs font simplement savoir à leur courtier quelles actions ils veulent, combien d’actions ils veulent, et généralement à une fourchette de prix générale. C’est ce qu’on appelle une « offre » et ouvre la voie à l’exécution d’une transaction. Si un investisseur veut vendre des actions, il indique à son courtier quelles actions vendre, combien d’actions et à quel niveau. Ce processus est appelé « offre » ou « demande de prix ».
Prédire comment le marché boursier fonctionnera est l’une des choses les plus difficiles à faire. Il y a tant de facteurs impliqués dans la prédiction — facteurs physiques par rapport au comportement physiologique, rationnel et irrationnel, etc. Tous ces aspects se combinent pour rendre les cours des actions volatils et très difficiles à prévoir avec un degré élevé de précision.
Machine learning en bourse
Les marchés boursiers et financiers ont tendance à être imprévisibles et même illogiques, tout comme le résultat de la Le vote sur le Brexit ou les dernières élections américaines. En raison de ces caractéristiques, les données financières devraient nécessairement posséder une structure plutôt turbulente, ce qui rend souvent difficile la recherche de schémas fiables. La modélisation des structures turbulentes nécessite des algorithmes d’apprentissage automatique capables de trouver des structures cachées dans les données et de prédire comment ils les affecteront à l’avenir. La méthodologie la plus efficace pour y parvenir est l’apprentissage automatique et le Deep Learning. Le Deep Learning peut traiter facilement des structures complexes et extraire des relations qui augmentent encore la précision des résultats générés.
L’ apprentissage automatique a le potentiel de faciliter l’ensemble du processus en analysant de grandes quantités de données, en repérant des schémas significatifs et en générant une sortie unique qui guide les traders vers une décision particulière basée sur les prix prédits des actifs.

Source : https://gifer.com/en/7JbT
Les cours des actions ne sont pas des valeurs générées aléatoirement, ils peuvent être traités comme un modèle de séries temporelles distinctes basé sur un ensemble d’éléments de données numériques bien définis collectés à des moments successifs à intervalles réguliers. Comme il est essentiel d’identifier un modèle pour analyser les tendances des cours boursiers avec des informations adéquates pour la prise de décision, il recommande que la transformation des séries chronologiques à l’aide d’ARIMA soit une meilleure approche algorithmique que la prévision directe, car elle donne des résultats plus authentiques et plus fiables.
Le modèle ARIMA (Autoregressive Integrated Moving Averge) convertit les données non stationnaires en données fixes avant de les travailler dessus. C’est l’un des modèles les plus populaires pour prédire les données de séries chronologiques linéaires.
Le modèle ARIMA a été largement utilisé dans le domaine de la finance et de l’économie, car il est connu pour être robuste, efficace et présente un fort potentiel de prévision à court terme du marché des parts.
Mise en œuvre des prévisions de cours des actions
d’Altaba Inc L’ensemble de données se compose de données boursières . téléchargé à partir d’ici.
Les données montrent le cours de l’action d’Altaba Inc de 1996—04—12 à 2017-11—2010. L’objectif est de former un modèle ARIMA avec des paramètres optimaux qui permettront de prévoir le prix de clôture des actions sur les données de test.
Si vous voulez en savoir plus sur l’analyse des séries chronologiques, je vous recommande de passer par cet article pour avoir une meilleure compréhension du fonctionnement de l’analyse des séries chronologiques.
Alors commencez par charger toutes les bibliothèques requises :
import os avertissements d’importation avertissements.filterwarnings (‘ignorer’) importer numpy en tant que np importer des pandas en tant que pp importer matplotlib.pyplot en tant que plt plt.style.use (« cinqtretreight ») à partir de pylab import RCParams RCParams = 10, 6 à partir de statsmodels.tsa.stattools, importer adfuller de statsmodels.tsa.saisonnier import seasonal_decompose à partir de statsmodels.tsa.arima_model import ARIMA de pmdarima.arima import auto_arima à partir de sklearn.metrics import mean_squared_error, mean_absolute_error importer des mathématiques importer numpy en tant que np
Chargez le jeu de données.
dateparse = dates lambda : pd.datetime.strptime (dates, ‘%y-%m-%d’) data = pd.read_csv (‘/Users/Nageshsinghchauhan/downloads/ml/time_series/stock-market/aaba.us.txt’, sep=’, ‘, index_col=’date’, parse_dates=, date_parser=dateparse) .fillna (0)
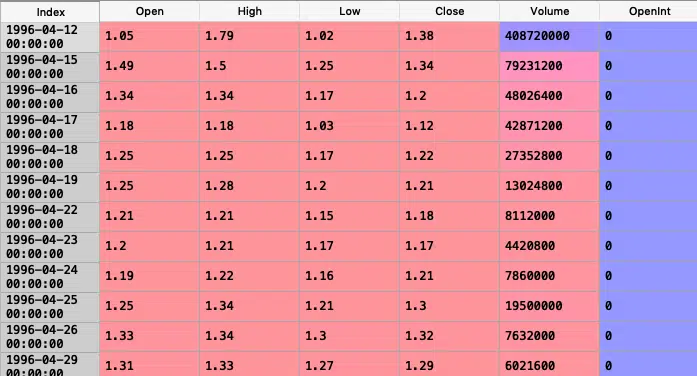
jeu de données
Visualisez le prix de clôture par jour de l’action.
#plot prix près plt.figure (figsize= (10,6)) plt.grid (Vrai) plt.xlabel (‘Dates’) plt.ylabel (‘Fermer les prix’) plt.plot (données) plt.title (« prix de clôture Altaba Inc. ») plt.show ()
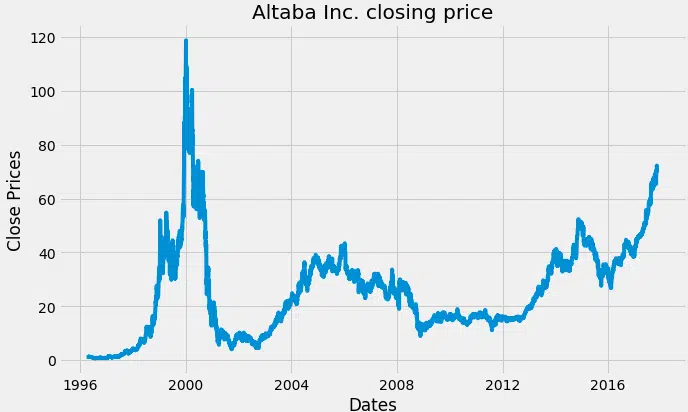
Prix de clôture d’Altaba Inc.
Permet de tracer le nuage de points :
df_close = données df_close.plot (style=’k. ‘) plt.title (‘Intrigue de dispersion du prix de clôture ») plt.show ()
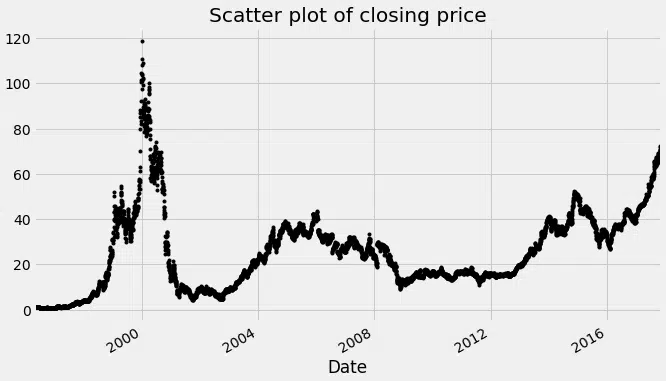
Diagramme de points du cours de clôture de l’action
Nous pouvons également visualiser les données de notre série à travers une distribution de probabilité.
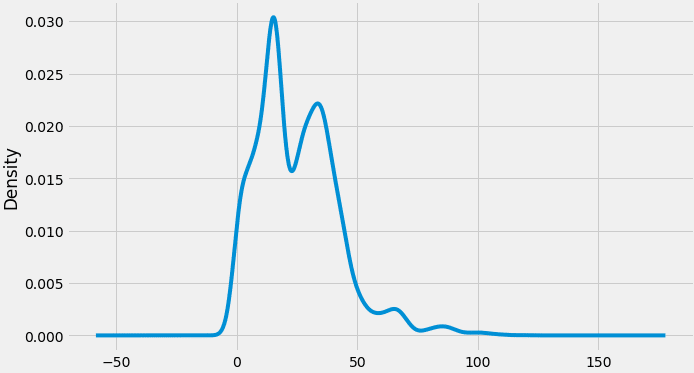
Répartition du stock de clôture prix
On croit également qu’une série chronologique donnée comprend trois composantes systématiques, dont le niveau, la tendance, la saisonnalité et une composante non systématique appelée bruit.
Ces composants sont définis comme suit :
- Niveau
- : Valeur moyenne de la série. Tendance
- : Valeur croissante ou décroissante de la série. Saisonnalité
- : Le cycle répétitif à court terme de la série. Bruit : Variation aléatoire dans la série.
Tout d’ abord, nous devons vérifier si une série est stationnaire ou non parce que l’analyse des séries chronologiques ne fonctionne qu’avec des données stationnaires.
Test ADF (Augmenté Dickey-Fuller)
Le test de Dickey-Fuller est l’un des tests statistiques les plus populaires. Il peut être utilisé pour déterminer la présence de racine unitaire dans la série, et donc nous aider à comprendre si la série est stationnaire ou non. L’hypothèse nulle et alternative de ce test est la suivante :
Null Hypothèse : La série a une racine unitaire (valeur de a =1)
Hypothèse alternative : La série n’a pas de racine unitaire.
Si nous ne rejetons pas l’hypothèse nulle, nous pouvons dire que la série n’est pas stationnaire. Cela signifie que la série peut être linéaire ou différentielle stationnaire.
Si la moyenne et l’écart-type sont des lignes plates (moyenne constante et variance constante), la série devient stationnaire.
Donc, vérifions la stationnarité :
#Test pour la staionarité def test_stationarity (séries de temps) : Statistiques roulantes #Determing rolmean = timeseries.rolling (12) .mean () rolstd = timeseries.rolling (12) .std () #Plot statistiques glissantes : plt.plot (séries de temps, couleur=’bleue’, label=’original’) plt.plot (rolmean, color=’rouged’, label=’Rolling Mean’) plt.plot (rolstd, color=’noir’, étiquette = ‘Rollstd’) plt.legend (loc=’best’) plt.title (« Moyenne mobile et écart type ») plt.show (bloc=false) print (« Résultats de test de dickey fuller ») adft = adfuller (séries de temps, AutoLag=’aic’) # sortie pour dft nous donnera sans définir quelles sont les valeurs. #hence nous écrivons manuellement quelles valeurs explique-t-il en utilisant une boucle for sortie = PD.series (adft, index=) pour la clé, les valeurs dans adft.items () : sortie = valeurs impression (sortie) test_stationarity (df_close)
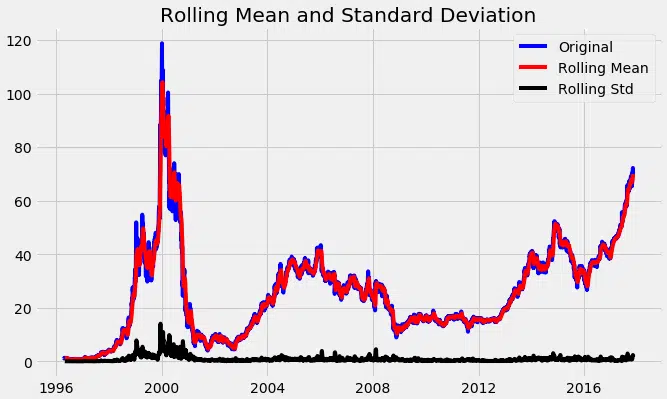
À travers le graphique ci-dessus, nous pouvons voir la moyenne croissante et l’écart-type et, par conséquent, notre série n’est pas stationnaire.
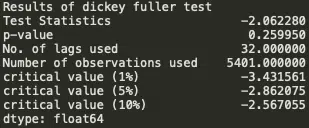
Résultats du test de Dickey-fuller
Nous voyons que la valeur de p est supérieure à 0,05, donc nous ne pouvons pas rejeter l’ hypothèse Null . En outre, les statistiques de test sont supérieures aux valeurs critiques. donc les données sont non stationnaires.
Afin d’effectuer une analyse de séries chronologiques, il se peut que nous devions séparer la saisonnalité et la tendance de notre série. La série résultante deviendra stationnaire grâce à ce processus.
Alors laissez-nous séparer Trend et Saisonnalité de la série chronologique.
result = seasonal_decompose (df_close, model=’multiplicative’, freq = 30) fig = plt.figure () fig = result.plot () fig.set_size_pouces (16, 9)
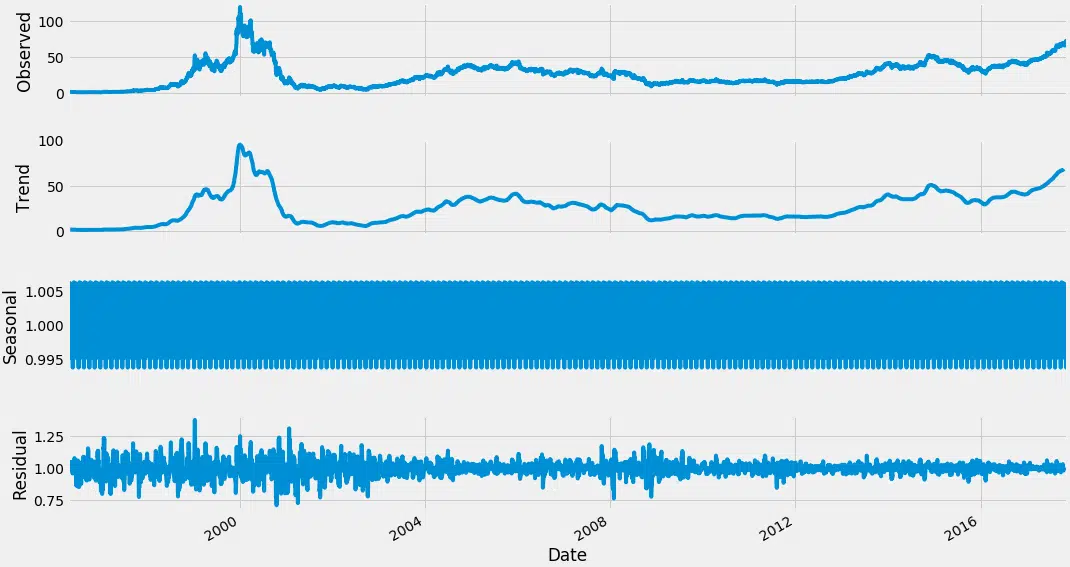
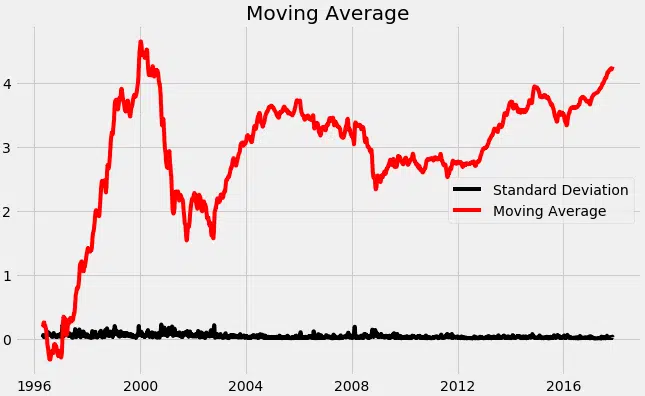
nous commençons par prendre un log de la série pour réduire l’ampleur des valeurs et réduire la tendance à la hausse dans la série. Ensuite, après avoir obtenu le journal de la série, nous trouvons la moyenne mobile de la série. Une moyenne glissante est calculée en prenant les intrants pour les 12 derniers mois et en donnant une valeur moyenne de consommation à chaque point plus loin dans les séries.
à partir de pylab import RCParams RCParams = 10, 6 df_log = np.log (df_close) moving_avg = df_log.rolling (12) .mean () std_dev = df_log.rolling (12) .std () plt.legend (loc=’best’) plt.title (‘Moyenne mouvement’) plt.plot (std_dev, color =”noir », label = « Écart type ») plt.plot (moving_avg, color=”rouge », label = « Moyenne ») plt.legend () plt.show ()
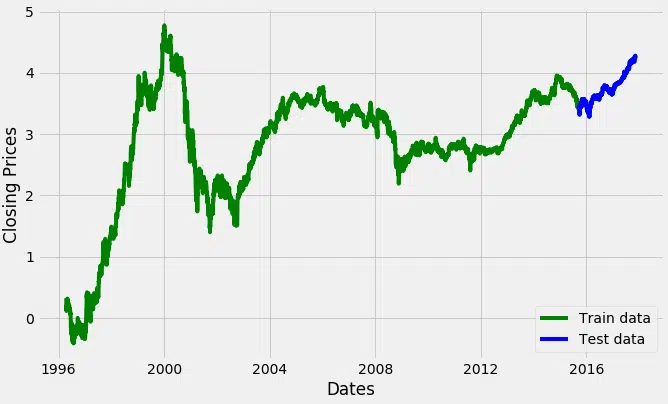
Maintenant, nous allons créer un modèle ARIMA et nous allons l’entraîner avec le prix de clôture de l’action sur les données du train. Alors divisons les données en ensemble de formation et de test et visualisez-les.
#split données dans le train et l’ensemble d’entraînement train_data, test_data = df_log, df_log plt.figure (figsize= (10,6)) plt.grid (Vrai) plt.xlabel (‘Dates’) plt.ylabel (« Prix de clôture ») plt.plot (df_log, ‘vert’, label=’données du train ‘) plt.plot (test_data, ‘blue’, label=’données de test ‘) plt.legend ()
Son temps de choisir les paramètres p, q, d pour le modèle ARIMA. La dernière fois, nous avons choisi la valeur de p, d et q en observant les tracés de ACF et PACF mais maintenant nous allons utiliser Auto ARIMA pour obtenir les meilleurs paramètres sans même tracer les graphiques ACF et PACF.
Auto ARIMA : auto_arima cherche à identifier les paramètres les plus optimaux pour un modèle ARIMA et renvoie un modèle ARIMA ajusté. Cette fonction est basée sur la fonction R fonction, Découvrez automatiquement la commande optimale d’un modèle ARIMA. La fonction prévision። auto.arimaauro_arima fonctionne en effectuant des tests de différenciation (c.-à-d. Kwiatkowski—Phillips—Schmidt—Shin, Augmenté Dickey-Fuller ou Phillips—Perron) pour déterminer l’ordre de différenciation, d , puis ajuster les modèles dans des plages définies start_p , max_p , start_q, max_q. Si l’option saisonnière est activée, auto_arima cherche également à identifier les paramètres optimaux P et Q hyper- après avoir effectué le Canova-Hansen afin de déterminer l’ordre optimal de différenciation saisonnière, . La fonction D.
Model_autoarima = auto_arima (train_data, start_p=0, start_q=0, test=’adf’, # utilisez adftest pour trouver ‘d’ optimal max_p=3, max_q=3, # maximum p et q m=1, # fréquence de la série D=aucun, # laisser le modèle déterminer ‘d’ Seasonal=faux, # Pas de saisonnalité start_p=0, D=0, traçe=true, error_action=’ignore’, suppress_warnings=true, stepWise=true) print (model_autoarima.summary ())
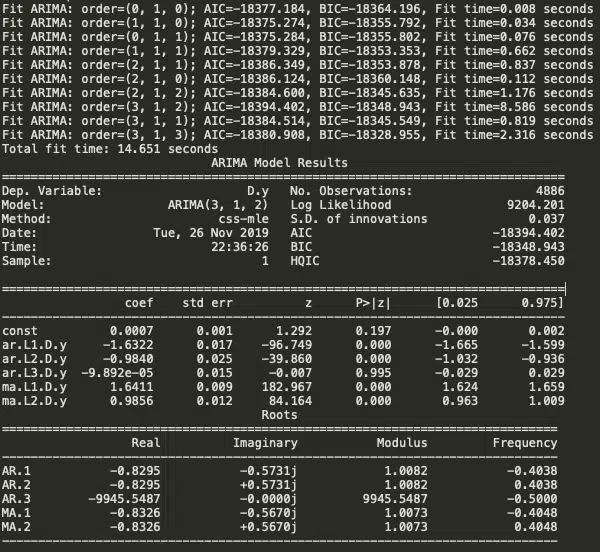
Ainsi, le modèle Auto ARIMA a fourni la valeur de p, d et q comme 3,1 et 2 respectivement.
Avant d’aller de l’avant, examinons les tracés résiduels de l’auto ARIMA.
Model_Autoarima.plot_Diagnostics (figsize= (15,8)) plt.show ()
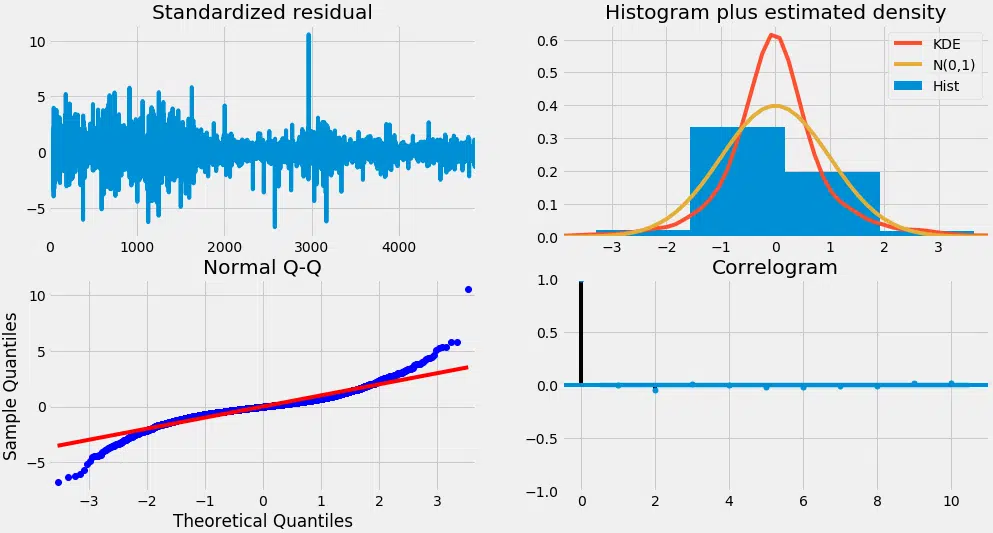
Alors, comment interpréter les diagnostics de l’intrigue ?
En haut à gauche : Les erreurs résiduelles semblent fluctuer autour d’une moyenne de zéro et ont une variance uniforme.
En haut à droite : Le diagramme de densité suggère une distribution normale avec zéro moyen.
Bas gauche : Tous les points devraient s’aligner parfaitement sur la ligne rouge. Tout écart significatif impliquerait que la distribution est asymétrique.
En bas à droite : Le Correlogram, alias, tracé ACF montre que les erreurs résiduelles ne sont pas autocorrélées. Toute autocorrélation impliquerait qu’il y a un motif dans les erreurs résiduelles qui ne sont pas expliquées dans le modèle. Vous devrez donc chercher plus de X (prédicteurs) pour le modèle.
Dans l’ensemble, il semble être un bon ajustement. Commençons à prévoir les cours des actions.
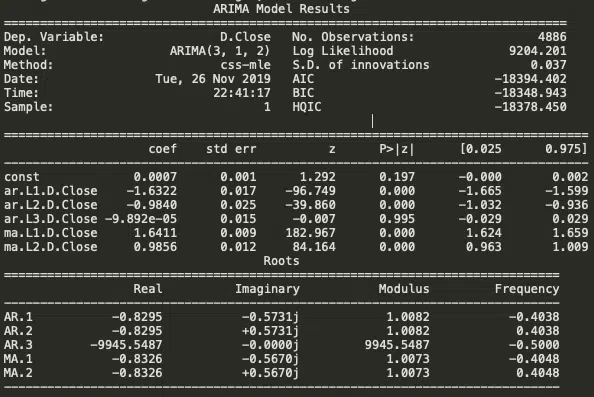
Ensuite, créez un modèle ARIMA avec les paramètres optimaux fournis p, d et q.
modèle = ARIMA (train_data, order= (3, 1, 2) ajusté = modèle.fit (disp=-1) imprimer (fitted.summary ())
Maintenant, commençons à prévoir les cours des actions sur le jeu de données de test en gardant un niveau de confiance de 95 %.
# Prévisions fc, se, conf = fitted.forecast (544, alpha=0,05) # Confiance à 95 % fc_series = PD.series (fc, index=test_data.index) lower_series = PD.series (conf, index=test_data.index) upper_series = PD.series (conf, index=test_data.index) plt.figure (figsize= (12,5), dpi=100) plt.plot (train_data, label=’training’) plt.plot (test_data, color = ‘bleu’, étiquette=’Prix du stock réel’) plt.plot (fc_series, couleur = ‘orange’, label=’Prix du stock prévisible’) plt.fill_between (lower_series.index, lower_series, upper_series, color=’k’, alpha=.10) plt.title (« Prévision du cours des actions Altaba Inc. ») plt.xlabel (‘Heure’) plt.ylabel (« Prix du stock réel ») plt.legend (loc=’en haut à gauche’, fontsize=8) plt.show ()
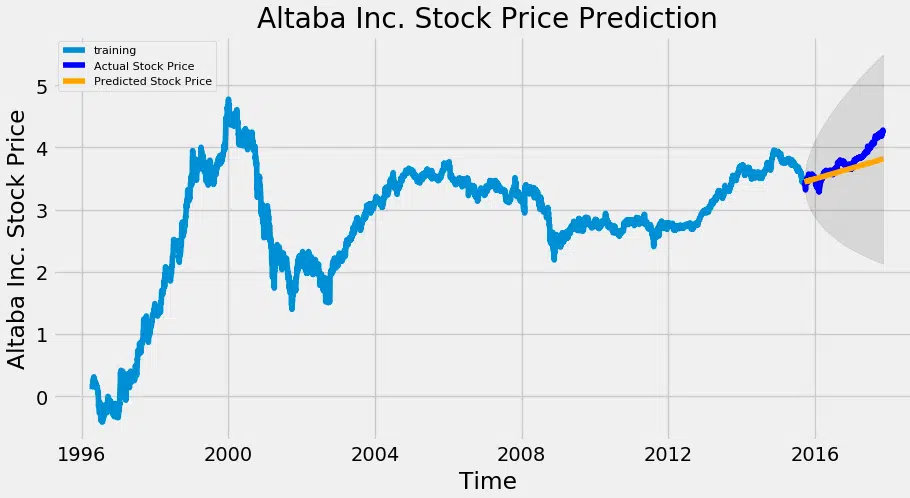
Comme vous pouvez le voir, notre modèle a fait assez beau. Vérifions également les mesures de précision couramment utilisées pour juger les résultats des prévisions :
# rapport de performance mse = mean_squared_error (test_data, fc) print (‘MSE : ‘ str (mse)) mae = mean_absolute_error (test_data, fc) print (‘MAE : ‘ str (mae)) rmse = math.sqrt (mean_squared_error (test_data, fc)) print (‘RMSE : ‘ str (rmse)) mape = np.mean (np.abs (fc – test_data) /np.abs (test_data)) print (‘MAPE : ‘ str (mape))
Sortie :
ESM : 0,03330921053066402 MAE : 0.13801238336759786 MSE : 0.18250811086267923 MAPE : 0.035328833278944705
Environ 3,5 % de MAPE (Mean Absolute Pourcentage Erreur) signifie que le modèle est précis d’environ 96,5 % dans la prévision des observations de l’ensemble d’essais.

Crédit : https://www.pantechsolutions.net/blog/artificial-intelligence-ai-projects/
Félicitations. Maintenant, vous savez comment construire un modèle ARIMA pour la prévision des cours des actions.
Conclusion
Dans cet article, les données ont été collectées sur kaggle.com. Les données historiques de 1996 à 2017 ont été prises en compte aux fins de l’analyse. La méthodologie BoxJenkins (modèle ARIMA) est formée et prédit les cours des actions sur l’ensemble de données de test.
Eh bien, c’est tout pour cet article espère que vous les gars ont aimé lire cela, n’hésitez pas à partager votre commentaires/pensées/commentaires dans la section des commentaires.

Source : diyuehb.com
Bio : Nagesh Singh Chauhan est un passionné de Data Science. Intéressé par le Big Data, Python, Machine Learning.
Original. Reposté avec autorisation.
connexes :
- Analyse du panier de marché : un tutoriel
- Introduction conviviale à la prise en charge des machines vectorielles
- Construisez votre premier Chatbot en utilisant Python et NLTK